2 Introduction

Harmonic analysis is commonly used to separate out periodic signals at tidal frequencies from more transient or irregularly occurring events. The calibration of hydrodynamic models for water level prediction relies heavily on tidal analysis. In particular, parametrizations for frictional effects used in barotropic storm surge models can be validated against tide predictions computed from harmonic analysis. In this blog post we describe two popular tidal harmonic analysis tools. We describe two differences between the packages, and quantify them for exemplary water level data. In a previous blog post, we analyzed tide gauge data from the north-eastern Bay of Bengal. The description of the software packages took up too much space, and we decided to move it to this separate blog post.

3 Scope

3.1 Harmonic analysis method and software packages

The general method of harmonic analysis based on the least squares solution is described e.g. in Foreman and Henry (1989). Given an observed time series $\zeta(t)$ of water level above a reference datum, one may define a predicted water level as

$$\zeta_{pred}(t) := Z_0 + \sum_{i=1..n}a_i\cos{\left(\omega_i t - \phi_{i}\right)},$$

where $n$ is the number of tidal constituents and $\omega_i$ the constituent's angular velocity. The objective is to find harmonic constants, i.e. amplitude $a_i$ and phase $\phi_i$ for each constituent (and the constant $Z_0$), such that the residual time series

$$\zeta_{res}(t) := \zeta(t) - \zeta_{pred}(t),$$

is minimal in a least-square sense. Amplitudes and phases may be modified by nodal corrections.

We use the SLP64 software package distributed by the University of Hawaii Sea Level Center, which includes the IOS Tidal Package written by Foreman (1977). The IOS Tidal Package in turn is based on the work by Godin (1972) and Godin and Taylor (1973). A secondary motivation of this blog post is to describe the general use of this FORTRAN software package and the related T_Tide MATLAB package of Pawlowicz et al. (2002), which is based on IOS Tidal Package but includes methods to compute confidence intervals and signal-to-noise ratios. One aspect in which the two packages are practically identical is the choice of tidal constituents that are included in an analysis.

3.2 Experiment with exemplary data

The exemplary tide gauge data for the experiment was measured at a station located in Chattogram (formerly known as Chittagong), Bangladesh. It is part of the inventory of the Joint Archive for Sea Level (JASL, see), maintained by the University of Hawaii Sea Level Center (UHSLC) (Caldwell et al., 2015). UHSLC distributes quality controlled, pre-processed hourly and daily water level.

4 Tidal constituents

The IOS Tidal Package includes 45 (24) astronomical (shallow-water) tidal constituents in its default configuration. The choice of main constituents is mostly based on the magnitude of the tidal potential amplitude.

Table 1: List of 45 astronomical constituents included in the default configuration of the tidal analysis package of Foreman (1977), sorted by increasing frequency. The constituent Z0 is a constant. The frequency is given in cycles per day. The constituent names are those used in the FORTRAN source code. Some of them encode a conventionally used Greek letter, e.g. *ALP1* stands for α, suffixed by the number 1, indicating that it is a member of the diurnal species. The Cartwright potential for each constituent can be found in tables A.1. and A.2 of Parker (2007), along with other important information such as synodic periods. A listing of shallow water constituents with frequencies identical to astronomical constituents can be found e.g. in Foreman and Henry (1989, their Table 4) and tables A.1. and A.2 of Parker (2007). For notes on naming conventions regarding H1 vs α2 see the text below and our previous blog post.
Const.	Freq. (cpd)	Const.	Freq. (cpd)
Z0	0.0000	THE1	1.0342
SA	0.0027	J1	1.0390
SSA	0.0055	OO1	1.0759
MSM	0.0314	UPS1	1.1122
MM	0.0363	OQ2	1.8234
MSF	0.0677	EPS2	1.8283
MF	0.0732	2N2	1.8597
ALP1	0.8255	MU2	1.8645
2Q1	0.8570	N2	1.8960
SIG1	0.8618	NU2	1.9008
Q1	0.8932	GAM2	1.9274
RHO1	0.8981	H1 (α2 *)	1.9295
O1	0.9295	M2	1.9323
TAU1	0.9350	H2	1.9350
BET1	0.9610	LDA2	1.9637
NO1	0.9664	L2	1.9686
CHI1	0.9713	T2	1.9973
PI1	0.9945	S2	2.0000
P1	0.9973	R2	2.0027
S1	1.0000	K2	2.0055
K1	1.0027	ETA2	2.0418
PSI1	1.0055	M3	2.8984
PHI1	1.0082

Table 2: As Table 1, but for 24 astronomical (shallow water) constituents included in the default configuration of the tidal analysis package of Foreman (1977).
Const.	Freq. (cpd)	Const.	Freq. (cpd)
SO1	1.0705	SK4	4.0055
MKS2	1.9377	2MK5	4.8673
MSN2	2.0363	2SK5	5.0027
MO3	2.8618	2MN6	5.7605
SO3	2.9295	M6	5.7968
MK3	2.9350	2MS6	5.8645
SK3	3.0027	2MK6	5.8700
MN4	3.8283	2SM6	5.9323
M4	3.8645	MSK6	5.9377
SN4	3.8960	3MK7	6.7996
MS4	3.9323	M8	7.7291
MK4	3.9377
S4	4.0000

Note that Parker (2007) may use a slightly different classification for astronomical vs. shallow water constituents. For example, H1 in Foreman (1977) seems to correspond to α2 in Parker (2007), who attributes neither the terms lunar, solar, nor shallow water to his α2. The constituent named SO1 is classified as lunar in Parker (2007) and associated with a shallow water equivalent which is apparently also named SO1. The constituent named MO3 is listed in Parker (2007) under the alternative name 2MK3 and classified as shallow water. Foreman (1977) notes that in all cases except SO1 and MO3, the main (rather than the compound) constituent is included in the standard constituent data package.

The choice of main constituents is mostly based on the magnitude of the tidal potential amplitude. For a listing of the "Cartwright potential" for all tidal constituents, see Cartwright and Edden (1973), or, perhaps more accessible, tables A.1. and A.2 in the appendix of Parker (2007). Foreman (1977) lists the potential in their tables 1-4. The program uses a lookup table that associates the length of a given time series with a predetermined set of constituents that can be analyzed. For a new candidate constituent with large Cartwright potential, the synodic period with respect to the closest "neighbouring" constituent (in frequency space) already present in the table (and hence even larger Cartwright potential), equals the required length of the time series to separate harmonic constants of the constituent pair. Foreman (1977) refers to the relationship between time series length and spectral resolution in this context as Rayleigh criterion. At runtime the user inputs a time series of given length, based on which the program automatically queries the table and thus determines the set of constituents to be included in the harmonic analysis. Details and exceptions to these guiding principles are given in Foreman (1977). The choice of shallow water constituents is based on a suggestion by Godin (Foreman, 1977, his section 2.1.2). Shallow water constituents are included in the analysis if the main constituents from which their frequency is derived, are included in the analysis, and if the time series is longer than the synodic period with respect to the constituent with larger amplitude that is closest in frequency. Parker (2007) points out in the legend of their table A.1. that for shallow water constituents it may not always be clear which nearby constituent should be compared with, presumably because their observed amplitude is even less directly related to a (Cartwright) tidal potential amplitude than this is the case for main constituents.

An explicit listing of the 45 astronomical constituents is contained in tables 1-4 of Foreman (1977). For data processing purposes, it is convenient to access the data directly from the input data files distributed with SLP64 (files ASTODATA and ASTOGDAT), IOS Tidal Package (files tide3.dat or tide5.dat) or VERSATILE_TIDANA . The information is contained in files , tide3.dat or tide5.dat in IOS Tidal Package, and Tide5n.dat in VERSATILE_TIDANA. The relevant section in these files contains the following data for each main constituent:

constituent name
Cartwright number
a phase correction (see p. 25 of Foreman, 1977)
number of satellite constituents for calculation of the satellite modulation, if applicable
If applicable, information on the satellite constituents for satellite correction follows each constituent within the same section.

4.1 Shallow water constituents

Shallow water constituents represent signals generated by the nonlinear interaction of the flow forced by main constituents. A listing of the 24 shallow water constituents included in the default configuration is given in Table 5 of Foreman (1977) and here in Table 2 above. The names and frequencies of the remaining shallow water constituents can be found in the aforementioned input data files (ASTOGDAT, tide3.dat etc.), which also encode information on how the shallow water constituent frequencies are computed from the main constituents. In general, shallow water constituents are formally derived for use in the package by calculating the effect of non-linear terms in the equations of motion due to main constituents. Foreman (1977) does not reproduce this derivation and cites pp. 154–164 of Godin 1972. The 24 constituents are derived only from the largest main constituents, i.e. M2 , S2, N2 , K2 , K1 and O1, using the lowest types of possible interaction (Foreman, 1977, their section 2.1.4). Complementing the reference to Godin (1972), which we have not been able to obtain, note also that Parker (2007) outlines the method of Fourier decomposition to determine which nonlinear mechanisms generate which compound tides and overtides in their chapter 7.6.

5 Differences between the packages

We note two differences between the IOS Tidal Package and T_Tide, with implications for our presentation of the residual time series.

The first difference is the way in which the packages apply nodal modulation corrections in their tidal predictions. We assume here that both analysis and prediction do not exceed intervals of about one year. The IOS Tidal Package apparently updates the amplitude and phase correction numbers (referred to as $f$ and $u$ in Foreman, 1977) for the prediction in monthly intervals, i.e. on the sixteenth day of each month (Foreman, 1977, their section 5). T_Tide, on the other hand, seems to hold the correction numbers constant during predictions, i.e. they are computed exactly once for the central point of the time series and are then applied to the entire interval. Below we give an example of the resulting differences.

The second difference is that along with the amplitude and phase for each constituent, T_Tide is able to compute confidence intervals or signal-to-noise ratios for each harmonic constant (Pawlowicz et al., 2002). One may choose to define some sort of statistical significance building on these quantities. Using the default parameters, t_tide.m computes bootstrapped confidence intervals based on an uncorrelated bivariate coloured-noise model. According to Pawlowicz et al. (2002), these allow a differentiation between "true deterministic (line) frequencies", and "broad-spectrum variability".

In its default configuration, the t_tide.m routine of T_Tide version v1.3_beta will include only significant constituents in the prediction of the water level, and hence also in the computation of the residual water level. One may generally define the residual as

$$\zeta_{res}(t) = \zeta(t) - \zeta_{pred}(t),$$

where $\zeta$ is the observed water level above a reference datum and $\zeta_{pred}$ is the prediction calculated from harmonic constants, i.e.

$$\zeta_{pred}(t) = Z_0 + \sum_{i=1..n}a_n\cos{\left(\omega_n t - \phi_{n}\right)},$$

$Z_0$ is the mean level above a reference datum over the interval of observation, $n$ is the number of tidal constituents, $a_n$ is the constituent's amplitude, $\omega_n$ is the angular velocity and $\phi_n$ is the Greenwhich phase (here in radians). Amplitudes and phases may be modified by nodal corrections.

In its default configuration, T_Tide will only use pairs of harmonic constants $\left(a_n, \phi_n\right)$ for which both constants have signal-to-noise ratio (SNR) larger than 2. This threshold can be modified when invoking the routine, and, if we interpret the comments in the code correctly, it seems that users are indeed expected to modify the threshold to study the sensitivity of the results. This is currently beyond our capacity and is deferred to future work.

On the other hand, the version of IOS Tidal Package distributed in SLP64 is configured to include all resolved constituents in the prediction, and hence in the computation of the residual. This gives rise to different definitions of the residual.

5.1 Data processing

In applying the method to the UHSLC data we loosely follow the steps outlined in chapter 4.5 of Parker (2007) and the manual of SLP64. We analyze time series of 366 consecutive days, as recommended in the SLP64 manual. For non-leap years, we choose the 365 days of the calendar year, and add the first day of the subsequent year. According to the constituent sorting strategy of Foreman (1977), the number of resolvable constituents with this length is 67, i.e. 44 main constituents (excluding the constant constituent Z0) and 24 shallow-water constituents. Note that the astronomical constituent Γ2 listed in Table 11 is not resolvable, since a time series of about 472 days would be necessary to separate it from H1 (α2) (Foreman, 1977, their Table 3). Table A.1. of Parker (2007) lists a Cartwright potential of -0.00273 for Γ2, compared to -0.00313 for α2.

As an example for the data processing, consider the year 2008. This is a leap year and hourly observations from 2008/1/1 00:00 UTC to 2008/31/12 23:00 UTC yield 366*24=8784 observations. Both IOS Tidal Package (provided with SLP64) and T_Tide will clip the last observation to obtain an odd number of observations (Foreman, 1977, their section 2.2.1).

6 Results

Figure 1 shows $\zeta_{res}$ at the Chittagong station (UHSLC ID 124a) for the year 2008. All other stations and years can be viewed in the companion blog post. The figure shows two different residuals, one calculated with the IOS Tidal Package and the other one with T_Tide. This is to highlight any possible differences arising from (1) the exclusion of non-significant constituents (as done by T_Tide in its default configuration), and (2) the different application of nodal correction numbers for predictions, as described above. The dashed green line in the figure shows filtered daily values obtained directly from UHSLC.

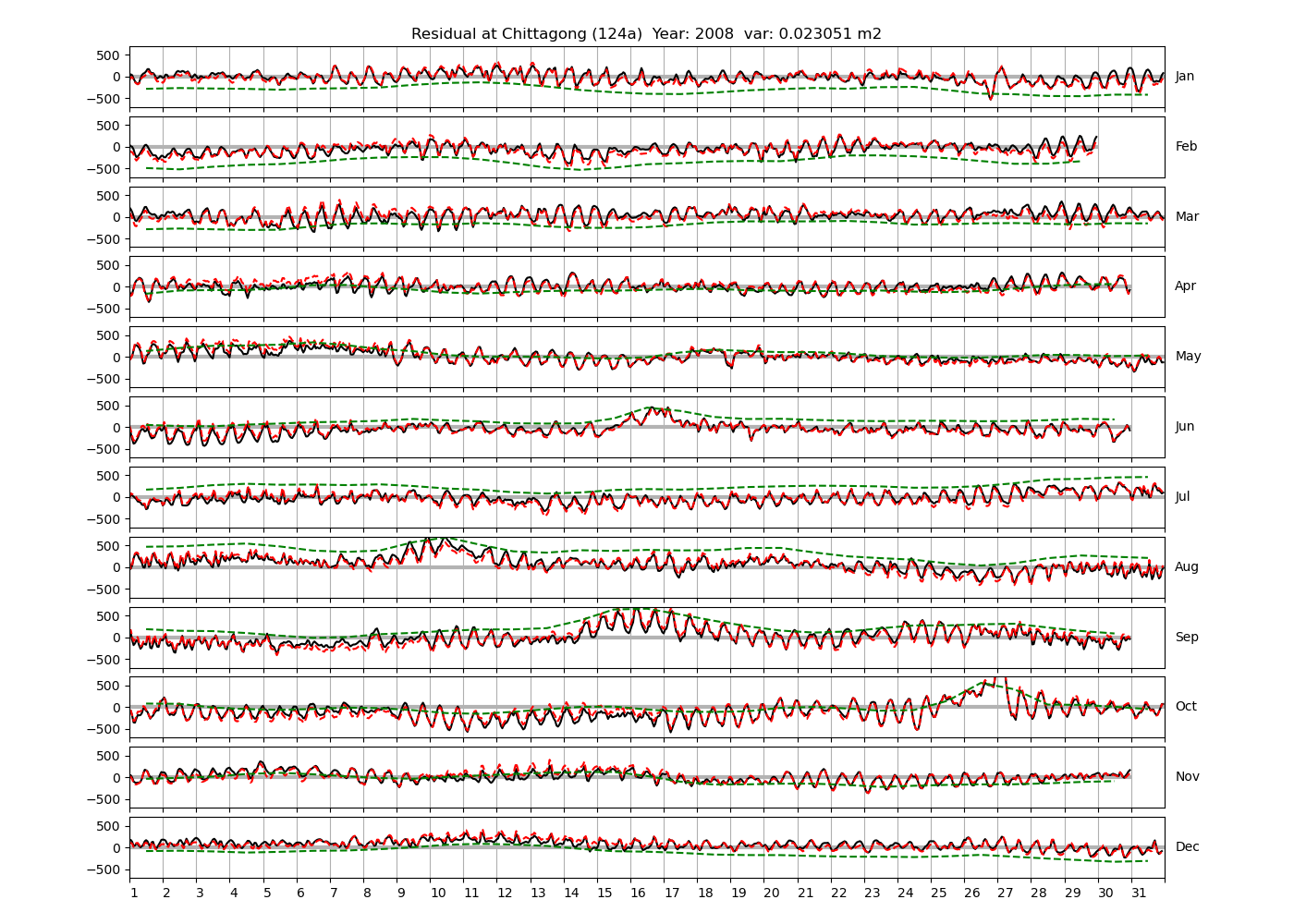
Figure 1: Residual sea level (in millimeters) at Chittagong for a 366 day interval covering the year 2008. The mean over the interval was subtracted. The **black** line shows the residual calculated with the IOS Tidal Package software distributed with SLP64 . The dashed **red** line shows the residual calculated with the default configuration of the T_Tide package, i.e. only harmonic constants above a signal-to-noise ratio larger than 2 are used for the predicted sea level. The figure is similar to the plots produced by the SLP64 package distributed by UHSLC. Here, the monthly means are not subtracted from the monthly residuals. The length of the calendar months is indicated by a gray bar at height zero. Also, the dashed **green** line shows filtered (de-tided) daily values obtained from UHSLC.

Figure 1: Residual sea level (in millimeters) at Chittagong for a 366 day interval covering the year 2008. The mean over the interval was subtracted. The **black** line shows the residual calculated with the IOS Tidal Package software distributed with SLP64 . The dashed **red** line shows the residual calculated with the default configuration of the T_Tide package, i.e. only harmonic constants above a signal-to-noise ratio larger than 2 are used for the predicted sea level. The figure is similar to the plots produced by the SLP64 package distributed by UHSLC. Here, the monthly means are not subtracted from the monthly residuals. The length of the calendar months is indicated by a gray bar at height zero. Also, the dashed **green** line shows filtered (de-tided) daily values obtained from UHSLC.

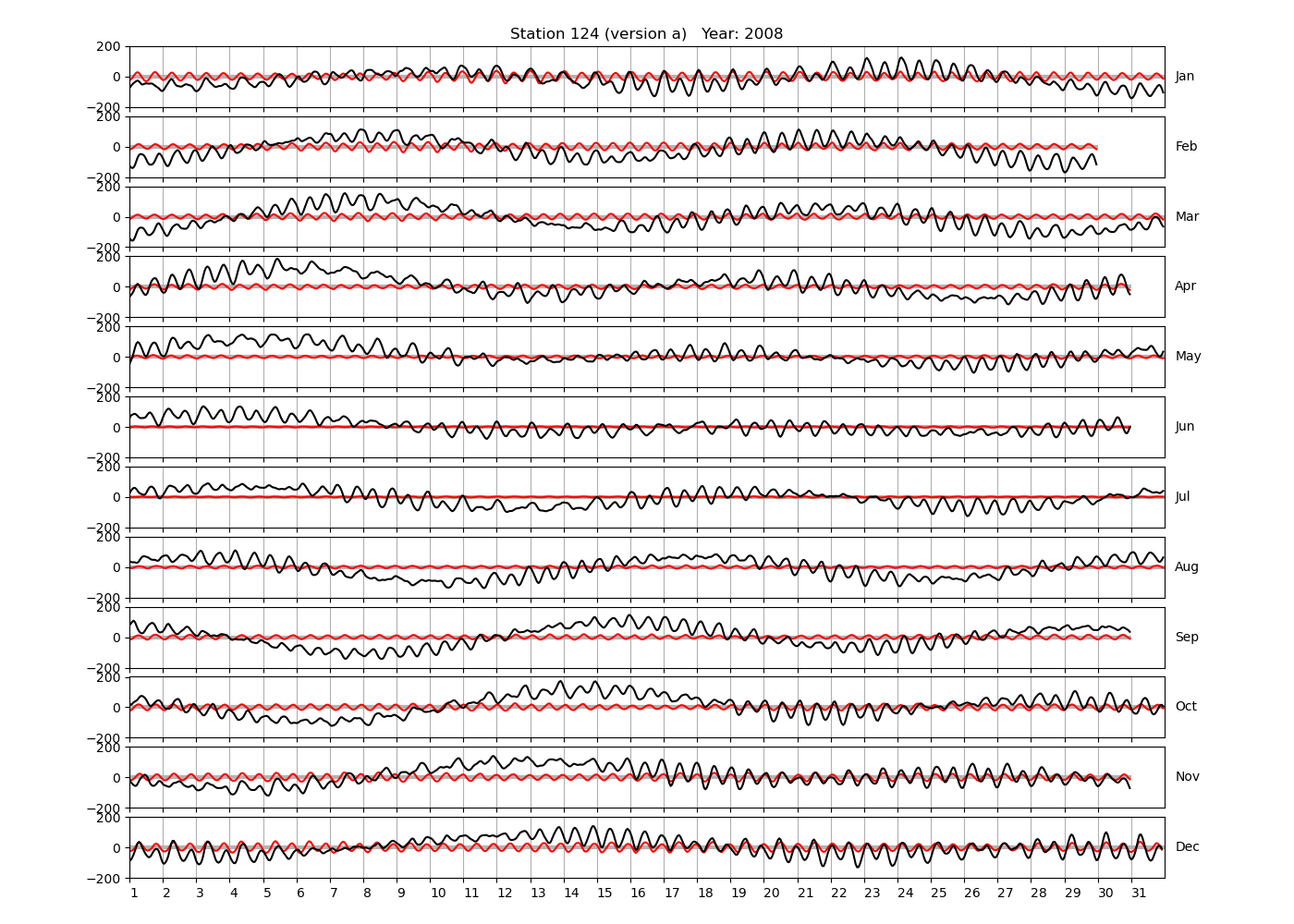
6.1 Difference between IOS Tidal Package and T_Tide

We plot the difference between the residuals for year 2008 at Chittagong in Figure 2. The black line is the difference between the residuals calculated with T_Tide and the IOS Tidal Package, which is equal to the negative difference between their predictions. The difference apparently has a fortnightly component, consistent with the fact that MSF (the lunar synodic fortnightly constituent) has the highest mean amplitude of all non-significant constituents (see the corresponding figure in the companion blog post).

To differentiate the effect of omitting non-significant constituents in the prediction of T_Tide from the effect of different strategies for nodal correction between the two packages, we re-compute the residual with T_Tide, but this time with all resolved constituents included. The red line in Figure 2 shows the difference between this new T_Tide residual and the IOS Tidal Package residual. The difference is nearly zero in June and July, i.e. around the center point of the interval, but up to about 5cm in magnitude over the entire interval. Shifting the time argument for the calculation of the nodal correction numbers from the center of the interval to another point has the expected effect, i.e. that the difference is nearly zero at the new anchor point (not shown). Computing the correction at the start or the end of the interval increases the magnitude of the maximum difference by roughly a factor of two. In any case, the effect of excluding non-significant constituents seems to have an overall larger effect on the residual than the details of the nodal correction.

References

Caldwell, P.C., Merrifield, M.A., Thompson, P.R., 2015: Sea level measured by tide gauges from global oceans — the Joint Archive for Sea Level holdings (NCEI Accession 0019568), Version 5.5, NOAA National Centers for Environmental Information, Dataset, doi:10.7289/V5V40S7W.
Cartwright, D.E., Edden, A.C., 1973: Corrected tables of tidal harmonics.
Foreman M.G.G, 1977: Manual for Tidal Heights Analysis and Prediction. Pacific Marine Science Report 77-10, Institute of Ocean Sciences, Patricia Bay, Sidney, B.C., 58 pp. (2004 revision)
Foreman M.G.G, Henry R.F, 1989: The harmonic analysis of tidal model time series
Godin, G., Taylor, J., 1973: A simple method for the prediction of the time and height of high and low water.
Godin, G., 1972: The Analysis of Tides.
Parker, B.B., 2007: Tidal analysis and prediction. NOAA Special Publication NOS CO-OPS 3, U.S. Department of Commerce, 378 pp.
Pawlowicz, R., Beardsley, B., Lentz, S., 2002: Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE.

Notes on tidal harmonic analysis software: The IOS Tidal Package and T_Tide

1 Abstract