A review of storm surge data for New York
Riha, S.1 Abstract
We review various data sources related to storm surge modeling around New York City, focusing particularly on data used in risk assessment and flood insurance regulations. A first objective is to review the physical significance of the National Flood Hazard Layer 
2 Introduction
New York City is an interesting region for storm surge modellers. It's a densely populated harbour city that experiences coastal floods caused by 1) extratropical "northeaster" storms and 2) former tropical storms (hurricanes) that curve northward along the U.S. East Coast and reach New York City. Parts of the city's coastlines face the open ocean and are exposed to direct wave action. Other parts are located within the New York Harbour, composed of several bays and complex waterways. The adjacent land is generally highly developed. While the harbor protects some regions from direct ocean waves, surges propagate into the harbor and can cause significant destruction. The hurricane Sandy event in 2012 is a recent example. Due to its geographical exposure, dense population and developed research infrastructure, the region is probably one of the most studied coastal flooding regions in the world. Assuming this is true, then why are we writing yet another blog post on this topic, instead of focusing on less developed regions of the world?
A primary motivation is simply to learn. Local and federal governmental agencies in the United States disseminate enormous amounts of useful information, both to the general public, and to teams of engineers and scientists which are contracted to make hazard mapping studies. Much of this information is publicly accessible, even from outside the United States. Best practices for coastal flood modeling established by the Federal Emergency Management Agency (FEMA) apply to other regions of the world. All of these factors make the U.S. in general, and New York City in particular, an attractive region to learn about storm surge modeling and to validate models or hypotheses.
However, the amount of publications, technical reports, guidelines, etc. available online from governmental
agencies like FEMA or the National Oceanic and Atmospheric Administration (NOAA) can
be overwhelming and difficult to process. It is difficult for a beginner to delineate the partly
overlapping, yet often seemingly disparate efforts that U.S. agencies pursue for storm surge risk assessment. For example, there are some projects aimed primarily at immediate emergency evacuation management, while others are targeted at long-term hurricane threat mitigation, regulatory and insurance purposes, etc. Currently, FEMA uses different numerical
models to cover the spectrum of applications
(e.g. USACE et al., 2011). To quickly get an
impression of the different inundation height estimates for a particular location, we maintain a simple (in no
way authoritative) prototype web app 

3 The National Flood Hazard Layer
FEMA promotes the National Flood Hazard Layer (NFHL) Viewer National Flood Hazard Layer (NFHL) Viewer 




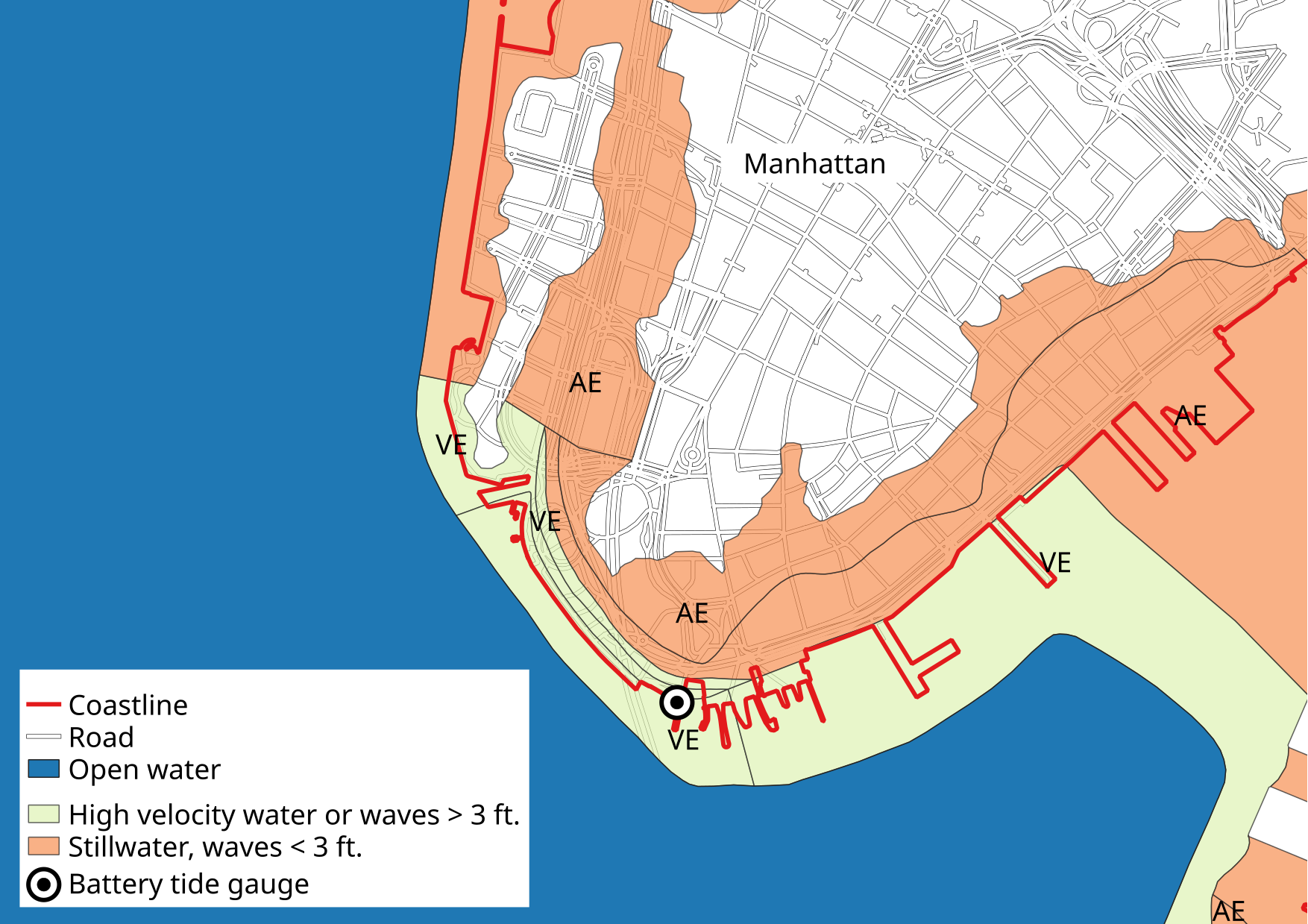
 .
.
Figure 2 shows base flood elevation (BFE) in feet for VE and AE zones. In coastal areas affected by waves, the base flood elevation includes effects of wave action, and effectively measures the height of the highest wave crests or wave runup, whichever is greater (e.g. FEMA 1998, their page 3-25). It is essential to note that this elevation is measured relative to a standard vertical datum, and not the local ground elevation. Elevations in the NFHL shapefile used here are referenced to the National Geodetic Vertical Datum of 1929 (NGVD 29). This can be somewhat confusing, since (FEMA, 2013) seem to use the North American Vertical Datum of 1988 (NAVD 88) throughout their most recent study. (Patrick et al., 2015) state that the transition from NGVD 29 to NAVD 88 was one of several updates brought by the 2013 Flood Insurance Study (FIS) as opposed to the previous study conducted in 1983. Base flood elevations in the NFHL are rounded to the closest whole foot.
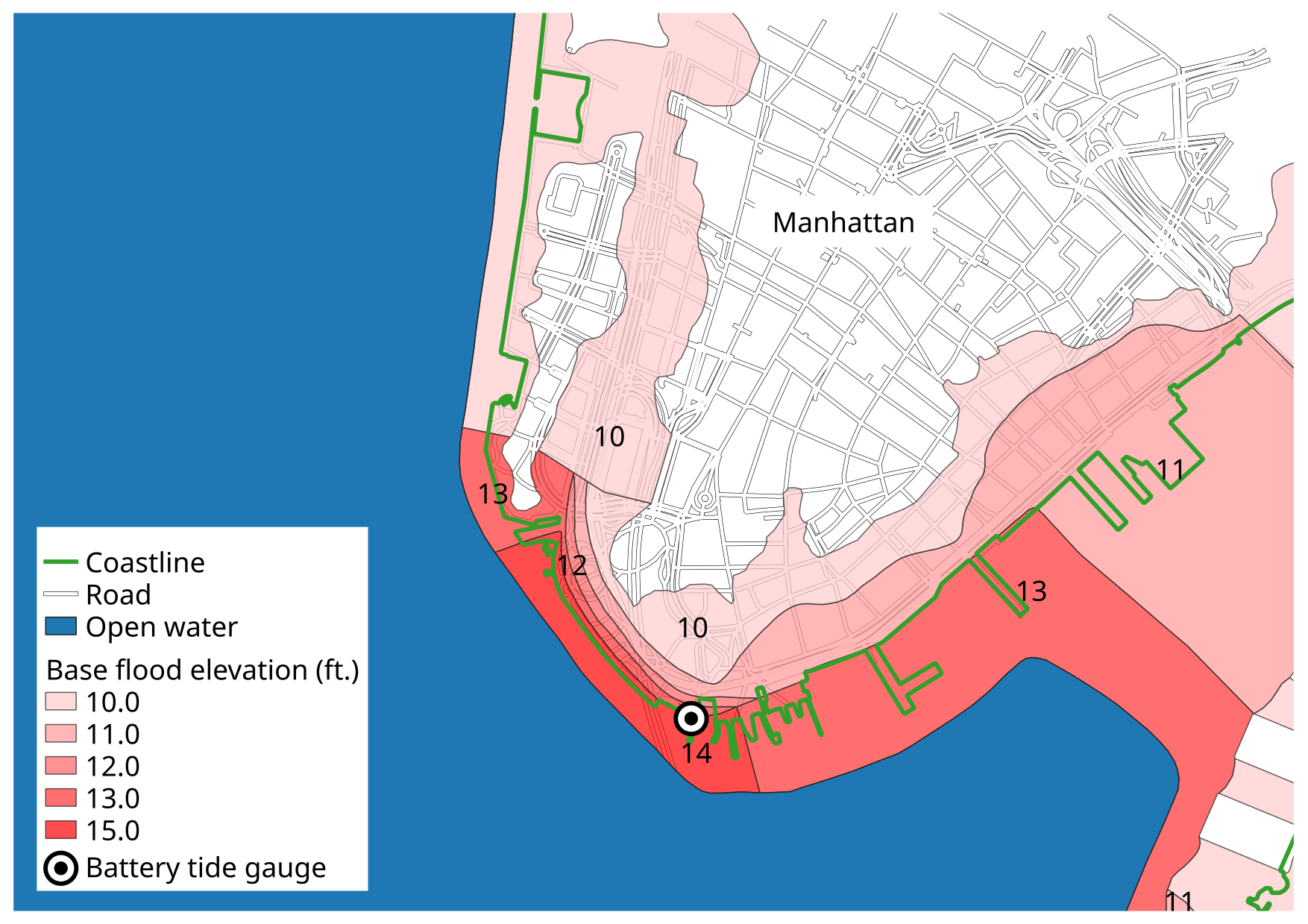
Figure 3 shows the
base flood wave crest height (or stillwater where applicable) above ground in feet. The wave crest height is computed as the difference between the
base flood elevation and the one arc-second USGS National Elevation Dataset (NED) 


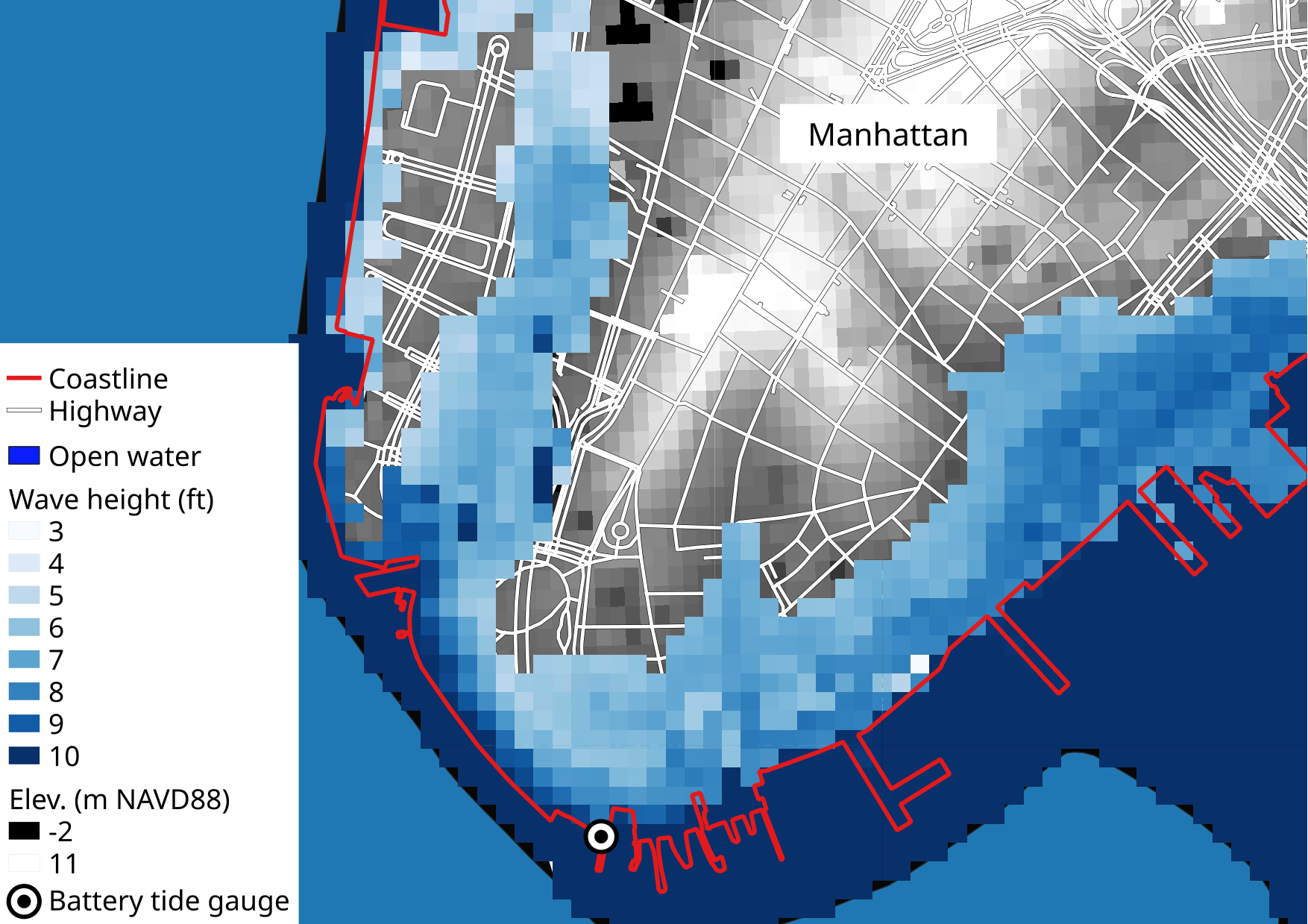
4 How does FEMA compute base flood elevations?
The second objective of this post is to summarize the methodology used to produce the NFHL data.
The currently available (2018/01/09) Preliminary Flood Insurance Study for the City of New York 


5 Analysis of stillwater return interval
To obtain probability distributions for water elevation, storm events are simulated using a numerical ocean model. Historical storm events are considered in the analysis if they caused flooding or exceed a certain intensity threshold. FEMA (2014b) analyze tide gauge data between 1950 and 2009, and rank storms based on the water elevation they caused along the coasts of New York and New Jersey. Of the most severe 36 storms, 30 were extratropical FEMA (2014b, see their p. 26). However, the two most severe storms where tropical in origin. Around New York, storms arriving from the tropics are apparently less frequent, but potentially more destructive than extratropical storms. In the following we sometimes refer to these storms as tropical storms, although they change their characteristics in higher latitudes and may more accurately be described as post-tropical cyclones. The lack of tropical cyclone data poses a problem for statistical analysis, since the sample size of the most destructive historical storms is very small. The approach taken by FEMA in the previous study for New York, is to artificially increase the sample size of tropical storms by constructing 159 synthetic storms. For extratropical storms this approach is not taken, perhaps not because a sufficient number of historical storms is recorded, but more because there seems to be ongoing scientific debate about defining appropriate controlling parameters (FEMA, 2014a, their p. 3). Hence, each historical extratropical storm is hindcasted. One can think of hindcasting as a synthetic replication that is strongly constrained to agree as closely as possible with available observed data.
Figure 4 sketches the individual steps for
determining the stillwater return interval. Stillwater is here
(as in FEMA, 2013, their p. 22)
defined as the water level including wave setup, i.e. averaged effects of
wave radiation
stress and breaking waves on the water level. The inclusion of wave setup in the definition of stillwater
is in line with the practice of fully coupling the SWAN wave model 

The preliminary result from the extratropical analysis is a Generalized Extreme Value (GEV) distribution, which yields stillwater elevation exceedance probabilities at each location of the modeling domain. To our knowledge, the full data set containing the fitted distributions at each individual point is not publicly available.
To give an
illustrative example for a GEV, one may instead use observed (non-synthetic) data available from NOAA. This also serves to establish contextual links between the synthetic NFHL data on the one hand, and observed extreme water levels published by NOAA, on the other hand.
NOAA (2013) analyze extreme water levels at several long-term tide gauges, to quantify probabilities of exceedance and the
return periods of extreme events based purely on observational (non-synthetic) data.
Figure 5
shows exceedance probabilities obtained by fitting a GEV to extreme residual water levels at the Battery tide gauge
located on the southern tip of Manhattan Island. The residual water level is the observed water
level minus the predicted tidal level at the time of observation. The units of the vertical axis are meters above
Mean
Higher High Water (MHHW) at the station. According to this site 


It is very interesting to note that Orton et al. (2015) state (on their p. 62) that the 1-percent chance flood is higher for extratropical storms than for tropical storms, if each of these groups is considered individually. So far we have not understood which results support this statement, and whether it refers only to their sea-level rise scenarios, or to the original FEMA report.
6 Extratropical storms
Figure 6 shows a
flow diagram sketching the computation of the stillwater return interval associated with extratropical
storms. The main task in preparing the forcing files for ADCIRC-SWAN is the manual hindcasting using "kinematic analysis"
FEMA (2014b). It is noteworthy that while a numerical model is used in the analysis of the post-tropical storm (see below), this does not seem to be the case for extratropical storms. It is interesting to speculate how sensitive the final GEV distributions are to the manual hindcasting, and whether useful results could be obtained by using e.g. the NCEP North American Regional Reanalysis (NARR) 
7 Synthetic post-tropical storms
Figure 7 shows a flow diagram sketching the computation of the stillwater return interval associated with post-tropical storms. A set of synthetic post-tropical storms was constructed following the Joint-Probability Optimal-Sampling Method (JPM-OS) outlined in FEMA (2012). For the creation of a representative data set, one needs to extract the typical physical properties of destructive post-tropical storms. Tropical storms were first filtered according to their proximity to the region FEMA (2014b, their p. 10).
In a second step, an intensity threshold was applied to
obtain a set containing 30 storms, which cover the range of parameter variations across the
region. The
intensity threshold was simply defined as an upper bound for minimum pressure
FEMA (2014b, their page 10). Hurricane tracks were obtained from HURDAT 
Wind speed was obtained from in-situ data, satellite data, reanalysis data, aircraft data, microwave radiometer, and other sources. The detailed formulation of their planetary boundary layer model remains unknown to us, but FEMA (2014b) state that their model is similar to the one described by Shapiro (1983). Contrary to several articles cited by FEMA (2014b), the latter is openly accessible. Along with the minimum pressure in the storm center, the model requires an estimate of the storm size and an estimate of the Holland-B parameter which reflects the "peakedness" of the wind and pressure profiles. The Holland-B parameter is obtained by a minimization procedure described on their page 14. However, they state that a prior estimate of the radius of maximum wind is required, and that estimate is obtained (quote:) "from the flight data with the best fit".
The estimated storm parameters describe the storm's characteristics at or near landfall. From a physical perspective, this is justifiable because storms are usually close to land (~200 km) when they cause significant surges. From a practical perspective, this is advantageous because observations near the coastline and on land are generally less sparse than in the open ocean (FEMA, 2014c, their page 2). A probabilistic characterization of future storms calls for a simple storm parameterization with few parameters. Most of the parameters vary with location, which accounts for the fact that hurricanes typically weaken rapidly along the northern U.S. East Coast (FEMA, 2014c, their page 12). A nice summary of the Joint-Probability Optimal-Sampling Method (JPM-OS) is given in (FEMA, 2012, see also their p. 13 for a quick overview of general JPM). They implement the JPM in several steps:
- They estimate the annual storm occurrence rate as a function of location and, optionally, heading. They estimate a probability distribution for heading. They only consider storms with a minimum pressure deficit of 33 mb (their p. 15). We speculate that the number of well-studied storms is too small to obtain robust rate statistics. Rates are counts over periods. In simple terms, a count is estimated as the distance weighted number of bypassing storms, where distance is defined as the minimal distance between the track and the point under consideration. The kernel function used to calculate the weights is Gaussian, with a standard deviation determined by an optimization procedure (FEMA, 2012, their p. 12).
- They estimate a spatially varying probability distribution for the pressure deficit. Here they use again storms with a minimum pressure deficit of 33 mb. They fit the scale and shape parameters of a truncated Weibull distribution to the observations, and use distance weighted averaging to obtain the dependency on geographical location. The uncertainty is estimated with a bootstrapping method, and as a final result they use a mean distribution which is well approximated by, but not identical to a proper Weibull distribution (their p. 16).
- They estimate a conditional probability distribution for the radius of the exponential pressure profile \(R_p\) (this parameter is similar, but not necessarily identical to the radius of maximum wind) from a subset of the 30 well-studied storms, which had satisfactory data quality or goodness of fit. They used a total of 19 storms (their table 3-1, p. 19). However, they do not fit a distribution to this data, presumably because it is too sparse. Instead, they use the data to validate a relationship formulated by Vickery and Wadhera (2008) for the median and standard deviation of \(R_p\) given the pressure deficit \(\Delta p\) (this is what makes the distribution conditional). They note that some authors have found a negative correlation between \(R_p\) and \(\Delta p\) (small radii are then associated with stronger storms), and that the presence or absence of such a correlation in the statistical model likely has large implications on the results. They state that allowing for large deviations of \(R_p\) from the median value is an important feature of the statistical model (their p. 18)
- They estimate the probability distribution of Holland's \(B\) parameter (Holland, 1980) simply by determining the mean and standard deviation of the pressure-profile fits from the hindcast simulations. They do not adopt the model by Vickery and Wadhera (2008) for determining \(B\), since it disagrees with their data.
- They estimate the probability distribution of forward velocity by determining a linear relationship for the mean value as function of \(\Delta p\), and a fixed standard deviation of 7 knots. The mean is capped to avoid unrealistically high propagation speeds. Based on a geographic trend visible in the hindcast simulations, they multiply the resulting forward speed by a factor that varies linearly with latitude, ranging from about 0.5 (at 30 degrees North) to 1 (at 40 degrees North).
Tracks are generated from one or more master tracks which are linearly interpolated to the location and heading of landfall (FEMA, 2014c, their page 19). The choice of individual master tracks is clearly visible in figure 27 of FEMA (2014b, their page 45), and in figure 4-3 of FEMA (2014c, their page 55). It is interesting that the orientation of the tracks seems relatively parallel, compared to e.g. the track of hurricane Sandy.
The steps outlined above are prerequisites for an application of the Joint-Probability Method (JPM), i.e. they yield a multivariate joint probability density function for storm parameters characterizing the study region. For a proper JPM, the entire support of the density function is discretized with a constant spacing along the parameter axes (\(\Delta p, R_p, \ldots\)). However, high resolution ADCIRC simulations are too computationally expensive for this approach to be implemented. Therefore, the parameter space is "optimally sampled" (OS) before the simulation runs, to extract the most interesting subsets of the parameter space. We defer a summary of the Optimal Sampling Method to a later post (see FEMA, 2012, for a more detailed description).
In browsing through the documentation published by FEMA, we have so far not found an explicit recipe of how they reconstruct the actual wind forcing from the parameters. We speculate that they use the same planetary boundary model that was used for the parameter extraction from historical observations (similar to the one described by Shapiro, 1983).
8 Related storm surge modeling efforts
We already mentioned a contextual link between NFHL data and NOAA's estimation of return periods based on observational data. Here we discuss some further differences between the FEMA flood insurance study on the one hand, and other modeling efforts aimed at forecasting and emergency response. This summary is limited to the differences between the wind forcing fields for the respective numerical models.
The SLOSH 
In a future post, we intend to review the effects of resolving mean wave effects explicitly with a model such as SWAN, which is current practice in FEMA flood insurance studies. If wave radiation stress (and breaking) are included in the model, then how sensitive are the results to details of the parameterized wind model? Is it sufficient to use the wind model of SLOSH, or is it worthwhile to use the more sophisticated profile generated by a planetary boundary layer model? Perhaps, probabilistic storm surge modeling and wind hazard modeling should be viewed as separate disciplines, each with different levels of sophistication for the wind model? Contact us if you are interested in this project.
9 Appendix
Our Figure 5 is similar to figure 29 of
NOAA (2013, their p. 196), who analyze extreme water levels at several long-term tide gauges
maintained by NOAA. Our data processing loosely follows theirs. Differences are discussed below.
We obtained hourly water level data for the Battery tide gauge 



-
We extract data from the Battery tide gauge only.
NOAA (2013) merge this data with a historic
tide gauge at Fort Hamilton (see their Table 2, page 15). They state that
All of the stations that were combined were placed on a common datum on the basis of a direct leveling connection to common benchmarks except for the Willets Point / Kings Point, NY series.
We did not attempt to reproduce this. It is currently unclear to us how the mean sea level and other tidal data is computed at the common benchmark. Furthermore, NOAA (2013) use data only through 2010 (or 2012). The different data sets necessarily leads to different parameter fits and return levels. Their estimate for the 0.01 exceedance probability (100 year return period) is 1.681 m, compared to our 1.792 (NOAA, 2013, their Table H, p. 195). Their estimate for the lower (upper) 95% confidence interval limit is 1.434 (2.173) m, whereas our estimate is 1.5066 (2.399) m. Note also that the different sample size leads to a lateral shift of dots representing individual observations (most clearly visible in the case of hurricane Sandy, which is shifted to the right in NOAA's figure relative to ours, due to their larger sample size). - We depart from an hourly time series retrieved from NOAA, whereas NOAA (2013) use 6-minutely intervals where available.
- We do not drop years with less than four months of data (cf. NOAA, 2013, their page 3). We have not quantified the consequences of doing this.
When comparing the return period estimates with data published by FEMA, one should keep in mind that the base flood elevations contained in the digitized National Flood Hazard Layer include all
wave
effects (not just wave setup), such as the height of individual wave crests. These heights are obtained from a
1-dimensional overland wave model, whose model domain is a set of transects placed orthogonally to the shoreline.
The 1-d model is forced with the stillwater height, and certain mean wave characteristics (obtained from
ADCIRC/SWAN) at the offshore end of the transect. To get this forcing data, in particular the stillwater
elevations, one can consult the more
detailed mapping transect data in the Flood Insurance Study for New York City
(FEMA, 2013). Their
Figure 1-2 shows the flood mapping transect map of New York County. Given the location of the Battery tide gauge 

10 Acknowledgements
The main contributors of data and background literature where U.S. govermental agencies, as acknowledged in the main text. The maps were prepared with QGIS 



References
- Fawcett, L., 2017: Chapter 2 of Lecture Notes for the MAS8391 MMathStat projects offered by Dr. Lee Fawcett, Newcastle University
- Federal Emergency Management Agency, 1998: Managing Floodplain Development Through The National Flood Insurance Program
- Federal Emergency Management Agency, 2007: National Elevation Dataset (NED) and Similar USGS Holdings
- Federal Emergency Management Agency, 2012: Joint Probability - Optimal Sampling Method for Tropical Storm Surge Frequency Analysis
- Federal Emergency Management Agency, 2013: Flood Insurance Study (preliminary). City of New York, New York.
- Federal Emergency Management Agency, 2014a: Region II Coastal Storm Surge Study: Overview
- Federal Emergency Management Agency, 2014b: Region II Storm Surge Project - Development of Wind and Pressure Forcing in Tropical and Extratropical Storms
- Federal Emergency Management Agency, 2014c: Region II Storm Surge Project - Joint Probability Analysis of Hurricane and Extratropical Flood Hazards
- Gilleland, E., Katz, R.W., 1983: extRemes 2.0: an extreme value analysis package in R. Journal of Statistical Software
- Holland, G.J., 1980: An analytic model of the wind and pressure profiles in hurricanes
- Jelesnianski, C.P., Chen, J., Shaffer, W.A., 1992: SLOSH: Sea, lake, and overland surges from hurricanes
- Kalnay, E., Kanamitsu, M., Kistler, R., Collins, W., Deaven, D., Gandin, L., Iredell, M., Saha, S., White, G., Woollen, J., Zhu, Y., 1996: The NCEP/NCAR 40-year reanalysis project
- Knaff, J.A., Zehr, R.M., 2007: Reexamination of tropical cyclone wind–pressure relationships
- NOAA Technical Report NOS CO-OPS 67, 2013: Extreme Water Levels of the United States 1893-2010
- Orton, P., Vinogradov, S., Georgas, N., Blumberg, A., Lin, N., Gornitz, V., Little, C., Jacob, K., Horton, R., 2015: New York City panel on climate change 2015 report chapter 4: dynamic coastal flood modeling.
- Patrick, L., Solecki, W., Jacob, K.H., Kunreuther, H., Nordenson, G., 2015: New York City Panel on Climate Change 2015 Report Chapter 3: Static Coastal Flood Mapping
- Shapiro, L.J., 1983: The asymmetric boundary layer flow under a translating hurricane
- U.S. Army Corps of Engineers (USACE), National Center of Expertise, 2011: TWO COASTAL FLOOD INUNDATION MAPS ‐ WHICH SHOULD I USE? HURRICANE EVACUATION STUDY ‐ STORM SURGE INUNDATION MAPPING VS. NATIONAL FLOOD INSURANCE PROGRAM ‐ FLOOD INSURANCE RATE MAP: An Overview and Comparison
- Vickery, P.J., Wadhera, D., 2008: Statistical models of Holland pressure profile parameter and radius to maximum winds of hurricanes from flight-level pressure and H* Wind data.